Calculador de LECER
Atención: Actualmente no hay LECER en el mercado. Dejo la información para realizar análisis sobre lo ocurrido en el pasado.
Calcular
Resultado:
|
FECHA LIQUIDACIÓN: 03/03/2026 - CER a fecha de Liquidación:
0,0000 |
| ESPECIE |
CER inicio |
VTO. |
PLAZO |
PRECIO C/ 100 VN |
TNA |
TIR |
DM (Días) |
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| Inflación Proyectada |
| 11-23 |
12-23 |
01-24 |
02-24 |
03-24 |
04-24 |
05-24 |
06-24 |
07-24 |
08-24 |
| |
|
|
|
|
|
|
|
|
|
| FECHA LIQUIDACIÓN:
03/03/2026 - CER de cada especie proyectado |
| ESPECIE |
VTO. |
CER inicio |
CER Proy. al vto. |
PRECIO C/ 100 VN |
TNA |
TIR |
DM (Días) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| MERCADO |
CURVA DE RENDIMIENTOS |
| ESPECIE |
PRECIO |
TIR |
DM |
precio de curva |
TIR de curva |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| MERCADO |
TASAS FORWARDS |
| ESPECIE |
TIR |
PLAZO |
PLAZO
T(n) - T(n-1) |
TASA FORWARD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Completar el calculador
Las LECER son explicadas en el apartado: LECER. En esta página tendremos un calculador que nos permita conocer los rendimientos.
Para utilizar el calculador debemos conocer lo siguiente:
- Fecha de liquidación: es el día en que se liquida la operación que concerté. Por ejemplo si el día 19/08/2022 compraba estas letras en el plazo de contado inmediato, se liquidaba el mismo día, por lo cual en fecha de liquidación debía ingresar el mismo día: 19/08/2022. En estas letras tenemos 3 plazos de liquidación: CI (contado inmediato), 24 hs y 48 hs hábiles. Si el día viernes 19/08/2022 compraba a un plazo de liquidación de 48 hs en fecha de liquidación debía ingresar el martes 23/08/2022.
- Comisión del agente: Es la comisión que nos cobre nuestro agente bursátil, que suele ser 0.2, 0.3 o 0.5%. Esta comisión la debemos ingresar para calcular el costo final que tendremos en el precio de las letras. Afecta mucho al rendimiento porque al ser letras de muy corto plazo el rendimiento en el período hasta el vencimiento es bajo, por lo cual si por ejemplo rinde un 1% en el período y el agente se va a quedar 0.5%, entonces el rendimiento que me va a quedar es la mitad. Mientras más lejana la fecha de vencimiento menos me afecta a la ganancia neta.
- Las especies de las letras son clave para conocer el vencimiento, ya que luego de la "X" inicial, me indica el día de vencimiento, la letra que sigue a los números indica el mes de vencimiento, y el último número indica el año de vencimiento.
- Proyectar inflación: Puedo cargar la inflación esperada por mí según mi opinión subjetiva, o tomar en cuenta alguna consultora, o bien la inflación esperada que se indica en el REM. Hay que tener en cuenta que podemos ingresar números con varios decimales, pero como pueden observar en la inflación pasada del BCRA obtenida del INDEC, solo se considera un solo decimal para conocer el aumento del Ft.
Explicación
Resultado
En el primer cuadro vamos a encontrar:
- El vencimiento de la letra, que depende del nombre de la especie.
- El plazo al vencimiento, que depende del vencimiento de la letra contra la fecha de liquidación.
- El CER de inicio, que es el CER de 10 días hábiles antes a la fecha de emisión.
- CER A Fecha De Liquidación: Es el CER de 10 días hábiles antes a la fecha de liquidación.
- El precio cada 100 VN, que depende del precio que indicamos y de la comisión de nuestro agente.
- TNA y TIR, que van a depender del valor final, del precio al que lo adquirimos, y del plazo restante al vencimiento.
- La duración modificada, que va a depender del precio, plazo y TIR de la letra.
A partir de la inflación proyectada vamos a encontrar:
- CER Proyectado a la fecha de vencimiento. Tener en cuenta que es el CER a la fecha de 10 días hábiles antes del vencimiento de la letra.
- Obtener la TNA, TIR y DM, pero al CER de vencimiento proyectando la inflación, y no al CER de liquidación como en el primer cuadro.
Curva de Rendimientos - también llamada Estructura Temporal de Tasas de Interés (ETTI)
Es el resultado que encontramos en verde dentro de la tabla, bajo el título "CURVA DE RENDIMIENTOS". Indica:
- TIR de Curva: Es la TIR que implicaría tener para encontrarse en la curva de rendimientos.
- Precio de Curva: Es el precio implícito que resulta de la TIR de Curva.
Tasas Forwards
Es el resultado que encontramos en verde dentro de la tabla, bajo el título "TASAS FORWARDS". Indica:
- Plazo: El plazo extra que tiene una especie, comparando el plazo de ella vs el plazo de la especie anterior.
- Tasa Forward: Es la TIR que debería tener en el plazo extra, para que rinda lo mismo comprar la especie anterior y reinvierto a ese plazo y tasa forward, que comprando esta especie directamente. Como puede ser confuso lo explico con números en el ejemplo debajo.
Ejemplo
Vamos a suponer que no tenemos comisión por comprar las letras. También suponemos que el precio del viernes 19/08/2022 fue el mismo que al cierre, y que estamos comprando al plazo de liquidación de 48 hs, lo que significa que en fecha de liquidación debo ingresar el martes 23/08/2022. La especie X16J3 no se había emitido a esa fecha por eso dejo el precio vacío.
Completar
Con esas premisas completo el calculador de la siguiente manera:
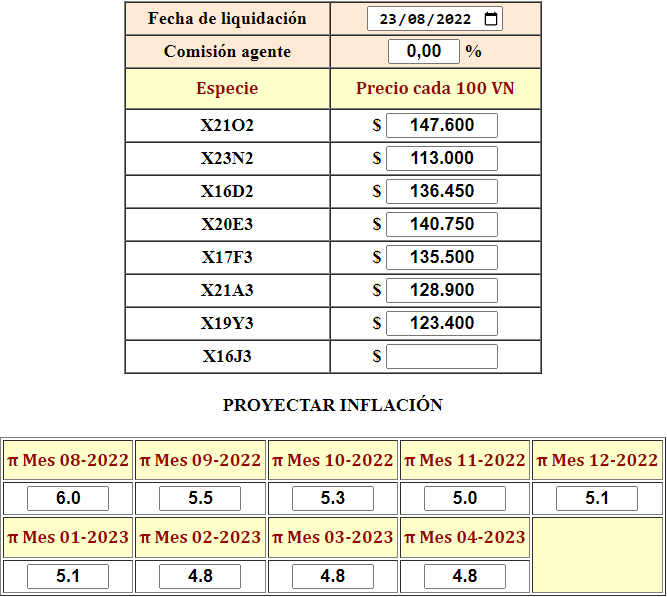
Resultado
Entonces el calculador me devuelve el siguiente resultado:
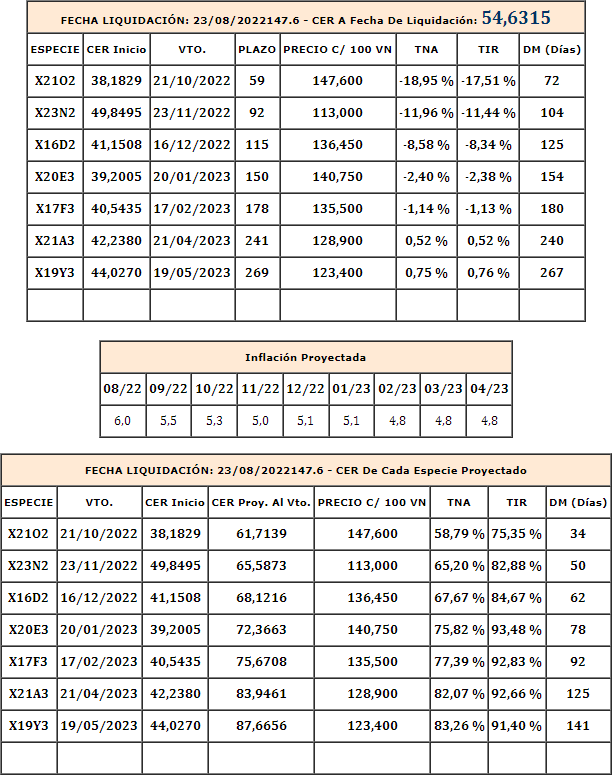
Si ingreso a ver el Informe de Letras del IAMC del día 23/08/2022 en el que informa rendimientos con liquidación a 48 hs, puedo observar que tiene el mismo resultado de TNA, TIR, DM y plazo al vencimiento de cada letra, con respecto a la primer parte calculada en la que no se proyecta el CER según la inflación que cargamos.
Curva de Rendimientos
La curva logarítmica de rendimientos tendría en esas DM las siguientes TIR e implícitamente esos precios.
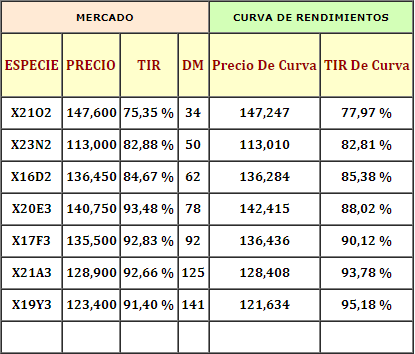
Tasas Forwards
A partir de las TIR de mercado que resultaron de los precios que cargamos, podemos obtener las tasas forwards, que significan cuánto deberían rendir en un plazo futuro las letras para que terminen rindiendo lo mismo que las otras. En este caso las comparo siempre contra la especie anterior.
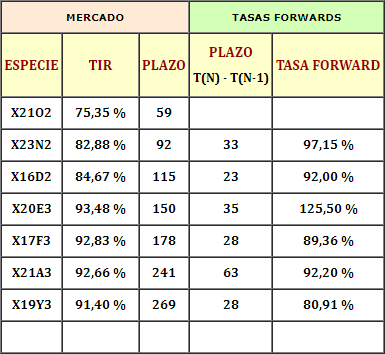
Para poner un ejemplo de lo que significa. Comparamos la primer LECER en el ejemplo que es la X21O2, con la X23N2.
Tenemos la siguiente ecuación:
( ( 1 + 0.7535 ^ (59 / 365) ) x ( ( 1 + 0.9715) ^ (33 / 365) ) = ( 1 + 0.8288) ^ (92 / 365)
1,095038698 x 1,063292767 = 1,164346728
El número 1,063292767 representaría el rendimiento forward de 6,3292767% de lo que invertimos en el futuro.
Para explicarlo en forma sencilla, la TIR de la X23N2 (82,88%) es más alta que la X21O2 (75,35%), por lo cual si invierto en la X21O2 necesitaría reinvertir el dinero en una TIR más alta que la X23N2 (en los 33 días que siguen al vencimiento del 21/10/22) para que me termine rindiendo en los 92 días lo mismo que la X23N2. Por eso, si en los primeros 59 días me rinde 75,35% necesito reinvertir (capital + intereses) y que en los restantes 33 días siguientes me rinda una TIR del 97,15% para que en los 92 días totales me terminen rindiendo igual que la especie X23N2 (82,88%).
En el ejemplo anterior:
- Si compro $ 1.000.000 en la X23N2 terminaría comprando (a un precio de $ 1,130) la cantidad de 884.956 VN, que al vencimiento (si no hay default) proyectando la inflación que indiqué (puede cambiar) serán al vencimiento $ 1.3157 por cada VN (CER de vto. dividido CER de emisión), entonces recibiré $ 1.164.336.
- Entonces para comparar supongamos que invierto $ 1.000.000 en la X21O2 (a un precio de $ 1,476), estaría comprando 677.507 VN, por lo cual al vencimiento proyectando la inflación que indiqué (puede cambiar) serán al vencimiento $ 1,6163 por cada VN (CER de vto. dividido CER de emisión), entonces recibiré $ 1.095.054. Para terminar con el mismo dinero que en el caso anterior ($ 1.164.336) necesito ganar $ 69.282 (es la resta entre $ 1.164.336 - $ 1.095.054), invirtiendo los $ 1.095.054 que tengo en ese momento, o sea necesito que mi rendimiento en ese período sea de 6,33% en los 33 días, ya que es la siguiente cuenta ( $ 1.164.336 / $ 1.095.054 ) - 1. Por lo cual la TIR sería: (1 + 6,33%) ^ (365 / 33) - 1 = 97,1%. Por cuestiones de redondeo en la TIR y en los valores nominales, no termina resultando totalmente exacto en este ejemplo.